June 15, 2022
•
...
Understanding Volatility, Delta, and Gamma is paramount to understanding options. For our purposes let’s assume that volatility is nearly linear to the price of an Option (which it is.) For the last couple of months, volatility has traded within a range around multi-year lows. This seemed to be a structural shift in market volatility which could have something to do with DOV’s or simply larger players entering the space to sell vol for premiums you can’t get in traditional markets. Either way, it’s become increasingly hard to make a living as a vol seller - until now, this blow up has led to volatilities we have not seen in a while.
Given the persistent low vol environment we’ve experienced over the last few weeks and the current high volatility priced in, we think it's only right to look at how you can potentially capture value in such an environment. For example, a strategy that is often used is simply selling puts or one could even sell a short strangle, so we will dive into both of those later on. Finally, we want to briefly talk about how Market Makers (MM’s) hedge short vega (vol) and gamma, and what effect their hedging potentially has on markets.
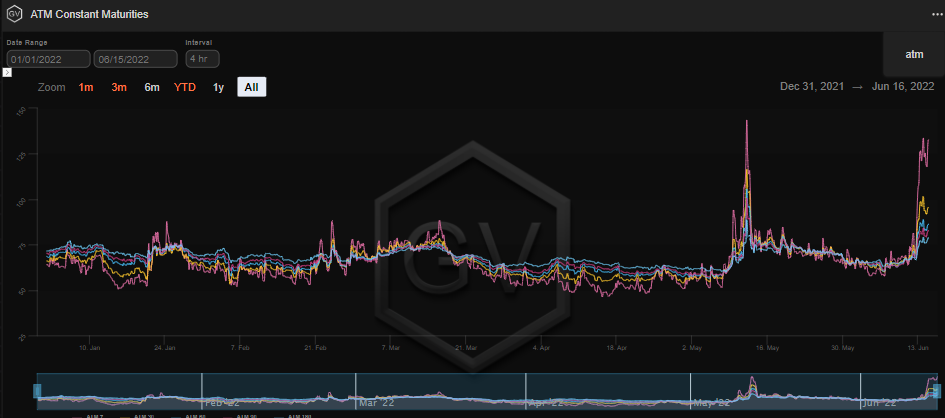
Looking at volatility year to date we can observe that the 3-month implied volatility traded between a range of 76-56 (until recently.) Selling vol at the higher end of the range over the last 4 months could have been a viable strategy. Of course you run the risk of vols blowing out like they have twice in the last month. Nevertheless, the strategy of choice during high IV environments is usually the short strangle, in-fact up until this recent volatility blowout a few funds we are in contact with were on track to do ~50% annualized. Some walked away unscathed, some gave up a good amount of what they had made to date, not all survived. I guess that’s a lesson right there, don’t get greedy, just survive.
For those of you unfamiliar, a short strangle is selling an OTM Put and Call at the same expiration date. You receive a premium upfront for accepting that risk which gives you your max profit, in other words you will never make more than the premium collected when putting on this trade. In the example below you would receive ~$3,200 per strangle. The potential risks can be quite dire if volatility were to spike, but with spot price ranging and volatility consistently being knocked down once it touched the mid-70’s, this is a great play, until it's not. You see this trade also means you have a potential for catastrophic loss to the upside and downside.
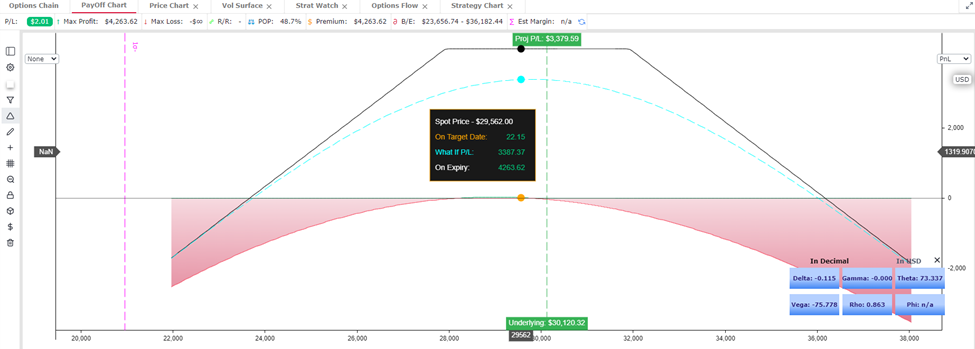
Hedging
Being that the short strangle is the weapon of choice used to collect premium at the moment. Selling (being short) volatility requires you to be short gamma.
This means two things, hedging can get quite expensive (if hedging dynamically,) secondly, hedging this position necessitates you to sell into crashes and buy into rally’s (more on that in a second.)
If you are a larger player, balancing one's book could mean moving the market further in the opposite direction than desired. Especially if liquidity is thin.
How does this work?
First, let’s look at how market makers might hedge.
Let’s say you sell an ETH Put $200 away from the money (0.30 delta.) You are now short 1 ETH put which means you are essentially long 0.3 ETH equivalent. The way to hedge this would be to sell 0.3 ETH via futures or perpetual.
As the market drops over a very small range the PV of the option will drop at .3 times the ETH itself, but because we are short the perp, the value of the perp will offset any loss our option has incurred. For that moment in time, we are fully hedged.
The problem is that over time the delta of the same option will change. Time plays a large role in the delta of an option over its life cycle. For example, the delta of an ETH Option $200 out of the money with one day till expiry is very small (maybe like 0.05 delta,) but the delta of that same Option with 6 months to run is more like 0.45 delta.
What does this mean?
All else being equal, as time passes the delta will be dropping (if it’s out of the money) and increasing if it’s in the money. At the same time spot price will be moving up and down, meaning as the OTM gets closer to ITM the delta increases, and inversely, it decreases as the option gets further away from being the money. We tend to ignore the time decay aspect because it’s slow, but it’s relevant.
The fact of the matter is if you hedge your downside by selling 0.3 of the perpetual contract and the option becomes ITM, delta would have risen during that transition and you would be underhedged.
So even though you are hedged at the beginning, you are no longer fully covered as time passes and the underlying moves. In our scenario, you would need to oversell to truly be hedged. For example, you would need to sell 0.4 of the perp to account for increasing delta as the underlying drops.
The second option being, you could dynamically hedge by increasing your negative futures position as you get closer and closer to the money. But doing this means you are behind the market because you are hedging the delta after it made its change, not before.
Additionally, if you were to over hedge from the start the market has the potential to move against you, in which case you would instantly be at a loss.

Gamma
We have now established that Market Makers need to hedge deltas, but how do they accurately predict how delta will move? As I am sure you are aware, Gamma is the first derivative of Delta, expressed as the rate of change of delta per 1 point move in the underlying. For example, if we have a 30-delta option with a gamma of 5, the market maker will have to re-hedge to a delta of 25 or 35 depending on how the market moves.
In the case of the 30d short strangle, we have a gamma total of -0.00359 and a total delta of -0.0264 at inception. If $BTC were to increase $1 in price, we would simply add our gamma to our delta leaving us with a delta of -0.02999. Our delta became more negative, which means, to re-hedge we need to buy delta using the perp. If $BTC decreases in price the opposite happens, our gamma becomes less negative meaning we need to sell the delta via the perp in order to rebalance.
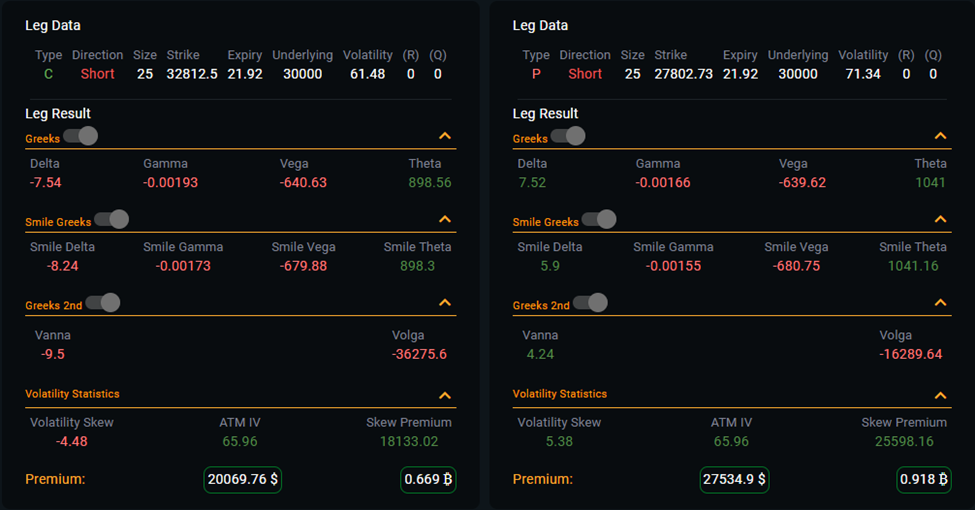
When large amounts of options are traded you can see how this might have an effect on the market. To hedge, negative gamma means you buy into rallies and sell into dips, if the size is great enough you exacerbate the move.
Currently, we are in the throes of yet another brutal sell off, as such, market participants are buying puts as insurance, which means MM’s are selling puts ie. selling vol. A MM’s position might look something like the below chart, short 1000x 20k Puts.
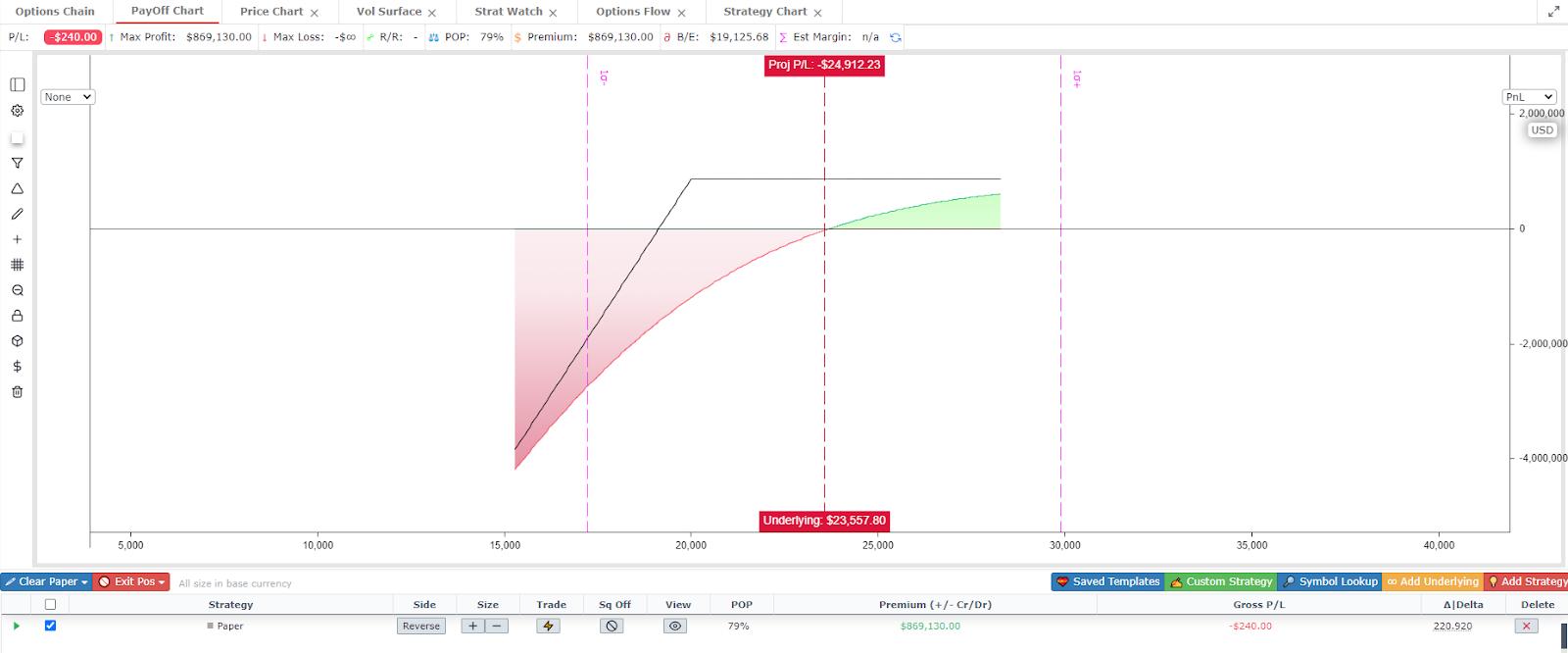
Their Gamma for this position is -.05 and their delta would be 223. If Bitcoin drops by $1000, the delta will increase by 50. The MM is now long too much delta, he is no longer hedged properly and needs to sell 50 perp contracts to rebalance. In a weak, thin, crashing market, this only serves to perpetuate the down move.
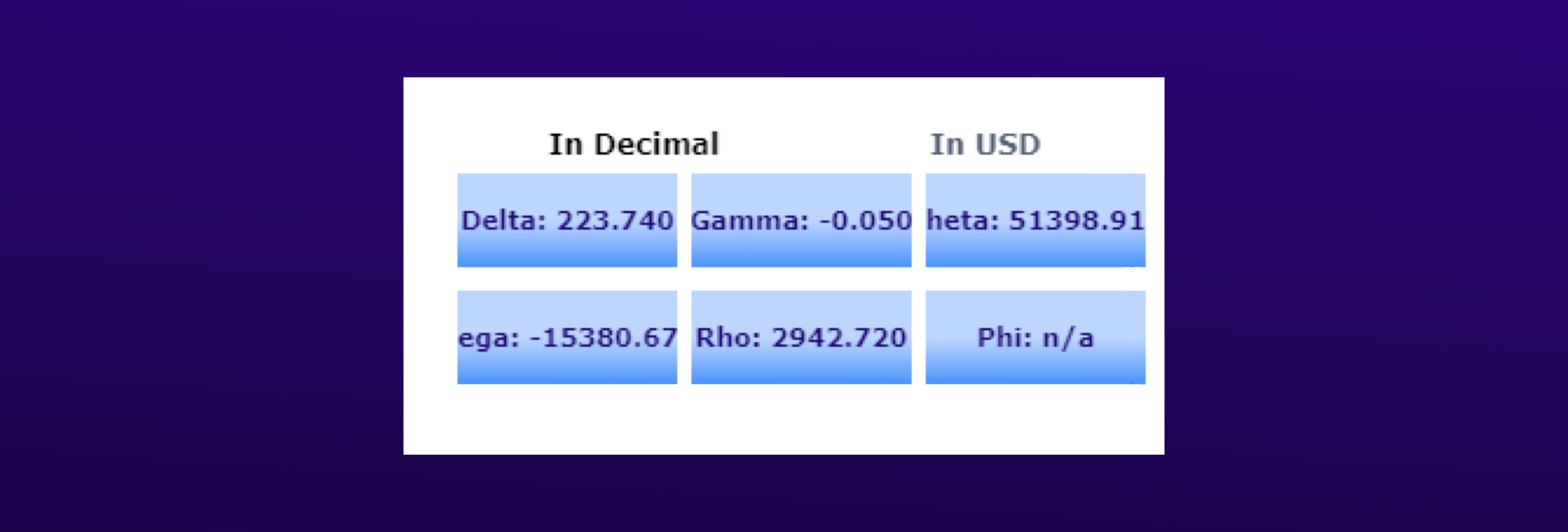
Note, the opposite is true of positive gamma, to hedge a positive gamma position you need to sell into rallies and buy the dips, thus dampening volatility, but I’ll leave you to work out the math.
Final Thought
When you are hedging negative Gamma you can never hedge it perfectly, you can only approximate at best. This is problematic in theory because it means that you will always be spending money on the hedge. Now, the short option should compensate you for this as its value decays over time, but the more you hedge the less you receive. In simpler terms, you are hoping the option is decreasing at a faster rate than it cost you to micro hedge.
Option pricing theory says that if an option is perfectly priced in a frictionless market you can hedge the option movement with infinitesimal trades over its lifetime and break even. This would also mean you priced the option perfectly with the correct volatility at the beginning. In reality, this is all impossible, markets aren’t frictionless, you have to pay spreads and trade fees, and there is no way you could hedge infinitesimally that quickly. So selling an option is truly pure risk that you can only hedge periodically. Remember, when hedging you are always crystalizing some loss.
Heading 1
Heading 2
Heading 3
Heading 4
Heading 5
Heading 6
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur.
Block quote
Ordered list
- Item 1
- Item 2
- Item 3
Unordered list
- Item A
- Item B
- Item C
Bold text
Emphasis
Superscript
Subscript





 @ResearchVariant
@ResearchVariant
